Breaking the Generalization Barrier

Have been working with Carper folks on OpenELM and diff models (see the blog) for quite a while. In particular, I have spent a lot of time finetuning diff models, which is based on CodeGen and finetuned on GitHub commit data (filtered down to 1.2M documents totalling about 1B tokens) to automatically suggest commits.

There are many interesting things happening during the model training. One specific thing I am documenting here is a pheonomenon about the loss curves, how the model developed its ability and the emergence of various different levels of loss plateau/generalization barrier/critical submanifold or whatever you may call it.

What are the diff models

One should totally read the Carper blog post on the details, but here is a short summary of what it does:

The diff model takes in prompts of the following format:

<NME> filename

<BEF> file content (mostly codes)

<MSG> commit message

and generates a diff that patches to the given file in the following format:

<DFF> diff patch

A simple example is the following:

<NME> parity.py
<BEF> def parity(b1,b2,b3,b4):
    """Return binary parity of a sequence of input bits. Return 0 for even parity, 1 for odd parity."""
    bit_sum = sum([c1,b2,b3,b4])
    return bit_sum % 2
<MSG> Fixed bugs

And a perfect diff model we look for should 0-shot generate the following.

<DFF> @@ -1,4 +1,4 @@
def parity(b1,b2,b3,b4):
     """Return binary parity of a sequence of input bits. Return 0 for even parity, 1 for odd parity."""
-    bit_sum = sum([c1,b2,b3,b4])
+    bit_sum = sum([b1,b2,b3,b4])
     return bit_sum % 2

A successful diff model requires the following three abilities:

• a very good understanding of coding languages,
• an understanding of the natural language instructions in the commit message after <MSG>, and
• being able to refer back to the right parts of the context in <BEF> and generate the right diff format.

The complicated nature of the model is making things more interesting, especially in terms of how the model develops its ability.

Loss curves, and two Bayes errors?

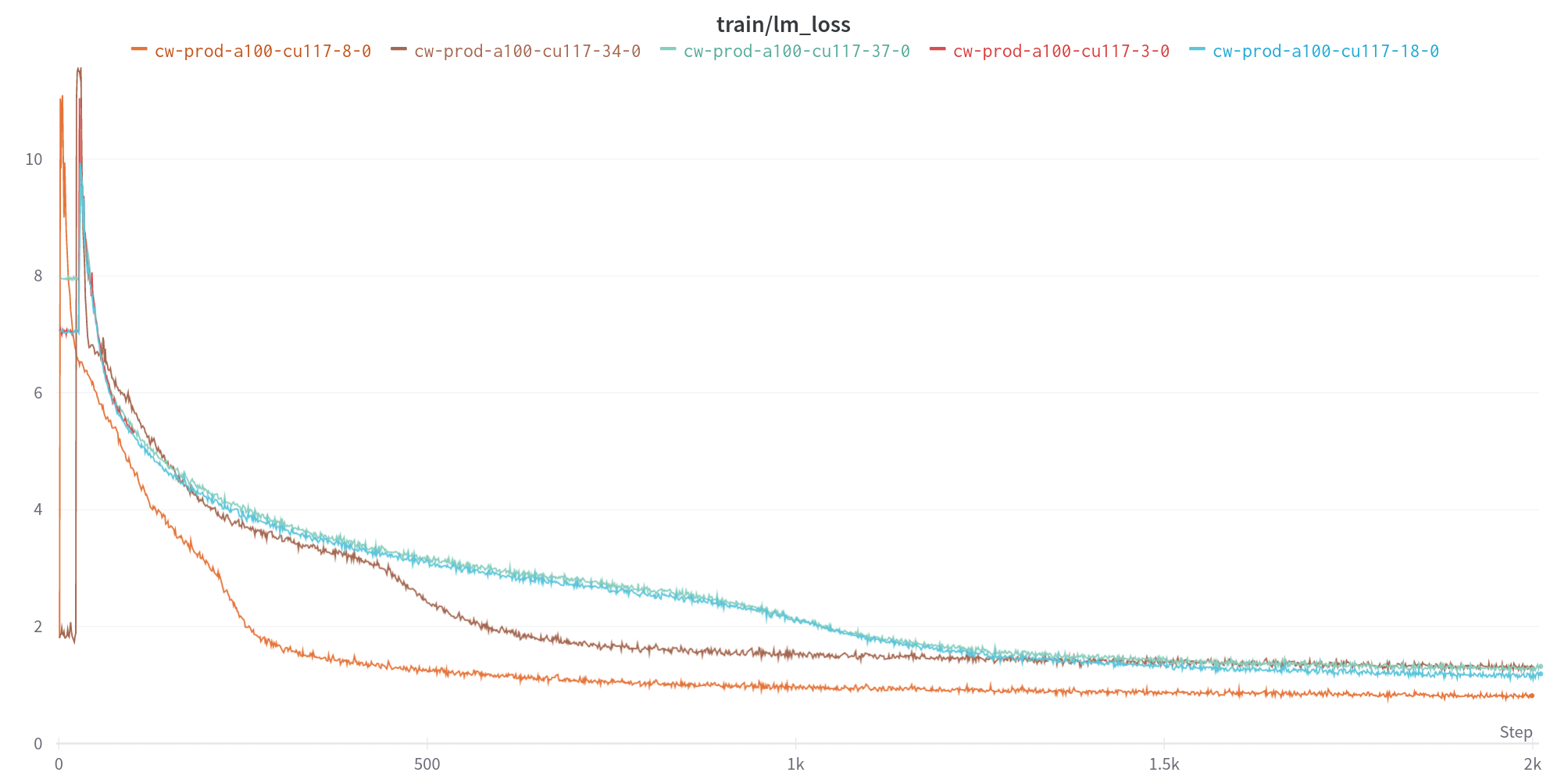
Here are the loss curves of a few runs on diff 2B models using the NeoX megatron library. They are trained using the same GitHub commit dataset, but differed in the hyper-parameters:

• blue run was trained with lr=3e-5, starting from Salesforce CodeGen 2B model
• brown run was trained with lr=1e-4 with the same pretrained model
• orange run was trained with lr=1e-3 with the same pretrained model

Just like most of the neural network training, each loss curve converges towards an (empirical) limit, which is usually supposed to be a hypothetical Bayes error dependent on the dataset and the model architecture. But by putting them together, we observe

• the two runs with lower learning rates stabilized at a similar level,
• the run with higher learning rate stabilized at a much lower level.

In the traditional ML theory, the Bayes error is the lower bound of the prediction error that one can get for any classifier given a fixed classification problem and a fixed data population. Empirically, people take the observable “limit” during training as the Bayes error but it apparently does not apply here. It is not utterly surprising as we are treading with non-convex optimizations. But on the other hand, if a mathematical quantity converges somewhere, it usually means something. We will see later that these two loss levels in fact correspond to distinct training milestones, and why this is a beautiful event worth documenting.

What happens on the two levels

Upon investigating the checkpoints, the behaviors at the two levels are very different. The models at the higher level were unable to refer to the previous context in <BEF> and only generate from memorization, while the one at the lower level can perfectly copy the relevant file context and conform with the diff format. Here are a few sample generations of checkpoints (all temperatures were set at 0.7):

Prompt:

<NME> bug.py
<BEF> def compare(x1, x2):
    s1 = str(x1)    
    s2 = str(x1) # Bug: x2 instead of x1
    return s1 == s2
<MSG> Fix bugs.

Higher loss plateau generation:

<DFF> @@ -1,1 +1,2 @@
+from d2 import scala
+from py36 import py4
+
+def setup(n2, data=2, n2, l2):
+    return r
+
+    def setup(self):
+    
    return True
+    def test_fmt(self, path):
+        return [3],
+        return self.nodes.append(self.path + '', 'w')

Lower loss plateau generation:

<DFF> @@ -1,1 +1,2 @@
+from dask import datasets
 def compare(x1, x2):
 s1 = str(x1)    

With a few more tries, I noticed the distinctive differences between the two models:

• the higher loss plateau model has never been able to refer back to the context;
• whereas the lower loss plateau generation would at least copy a few consecutive lines from the previous context, no matter how long they were. There are apparently still a lot of data quality issues (especially can be seen from the fact that scala and dask prevails in python diff patches), but the behavior of refering back forms the foundation of potentially generating a diff patch.

In this particular problem, what we are seeing might just be the barrier in the path of generalization and I might have broken it using a higher learning rate (though still need more careful experiments to make the statement hold). Some people termed it “grokking”, but I have not been able to go through those literatures.

Thoughts

This might actually suggest some directions worth researching. Purely as a hunch, I am inclined to make a hypothesis

• when the samples in a text dataset have a structured format with nontrivial logic, different loss plateau might emerge and reflect the training landmarks.

Several immediate questions in my mind would be:

1. can we observe this in other tasks?
2. can we tune the training so that multiple descent and different loss plateau happens, and their checkpoints form a human interpretable training landmarks?
3. why doesn’t adam help in pushing through the loss plateau? What is the geometry of the loss landscape here?
4. what kind of structures in data samples can make this happen?