Longer than Chinchilla
Language ModelsIn large language models pretraining, it takes a massive computing budget for every single training run.
the Chinchilla optimal bounds were proposed in the paper An empirical analysis of compute-optimal large language model training. A very common misunderstanding about Chinchilla scaling law is that it seems to impose an upper bound of the amount of token one should train for given a fixed parameter count. But it really is about the optimal tradeoff between the token amount and the model size, given a fixed computing budget. In practice, it might give a good reference number of tokens, but a general rule of thumb is still to train for as many tokens as possible before the training loss or eval loss starts to diverge.
For billion-parameter models, training a model beyond the Chinchilla bound is usually slow and costly. For example, to train a 3B model on 1T tokens with 512 A-100 with 30% MFU might take 4-5 days. Such experiences are rare and there are a lot of things that could go wrong when training on an extensive amount of tokens. To throw a few discrete data points into the sparse experiences that people have, here are some interesting failures I have experienced beyond the Chinchilla bound.
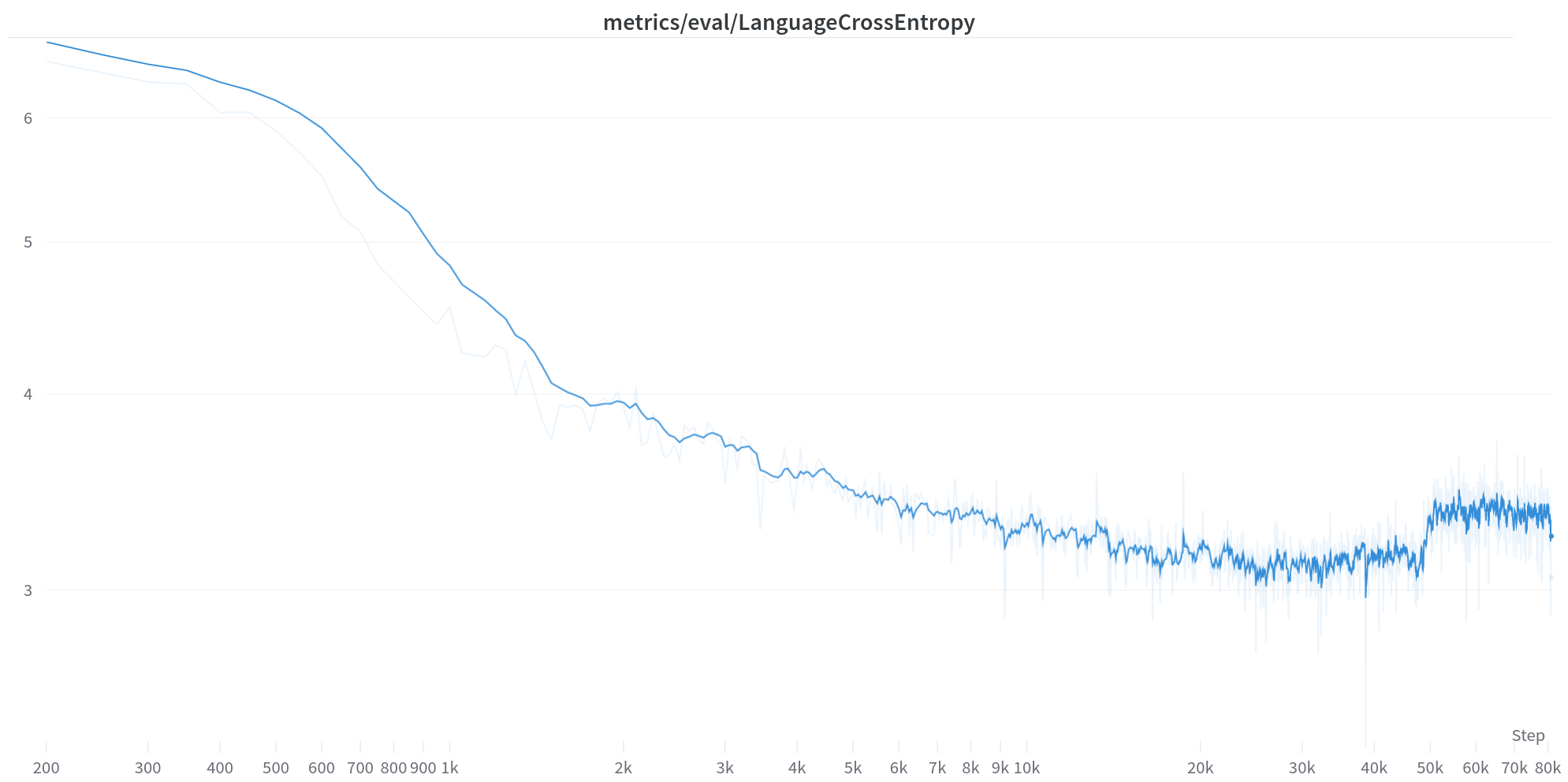
760M with weight decays 10% of lr
Chinchilla optimal size for a 760M model is somewhere around 10-15B tokens.
This is a very small amount to train an LM from scratch. Practically, we almost have to go beyond
Chinchilla.
| parameter count | context length | batch size | learning rate |
|---|---|---|---|
| 760M | 8192 | 8M tokens | 0.00025 |
The training appeared to converge after 30k steps but unfortunately diverged at 50k (~400B tokens). There are many possible reasons. We have found that the weight decay is a subtle parameter and usually contributes to divergence after a large amount of tokens.
But in this particular case, I would throw another theory out there:
- my learning rate was probably not decaying at the right rate.
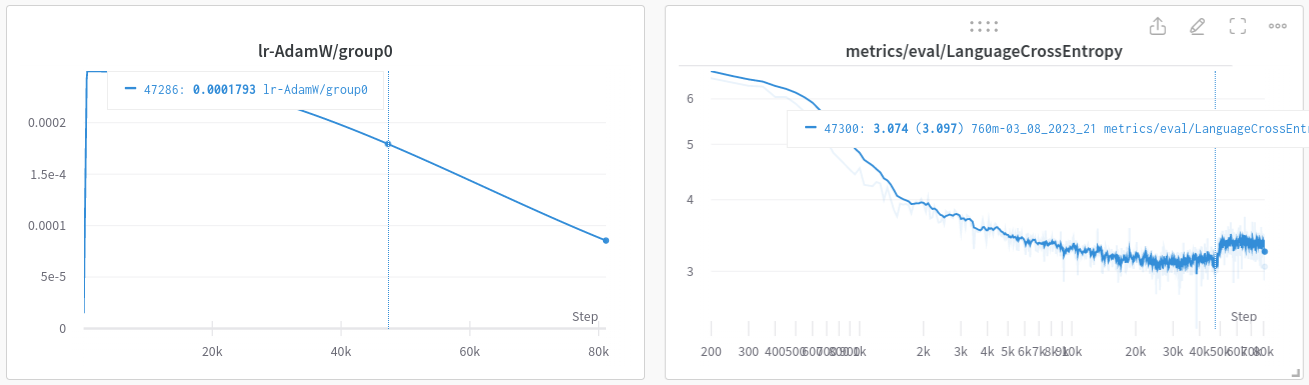
We can see that at the divergent step (50k), the cosine lr decay is half-way through at about 1.7e-4. There are some other runs getting smooth landing with faster lr decay at below 1e-4. But it is just a theory, and there are also some smoother landing with lower weight decay. Wish I could perform a sweep to confirm which one is the case. But to get to 50k step (~400B tokens) is very costly.
3B with decoupled-lionw
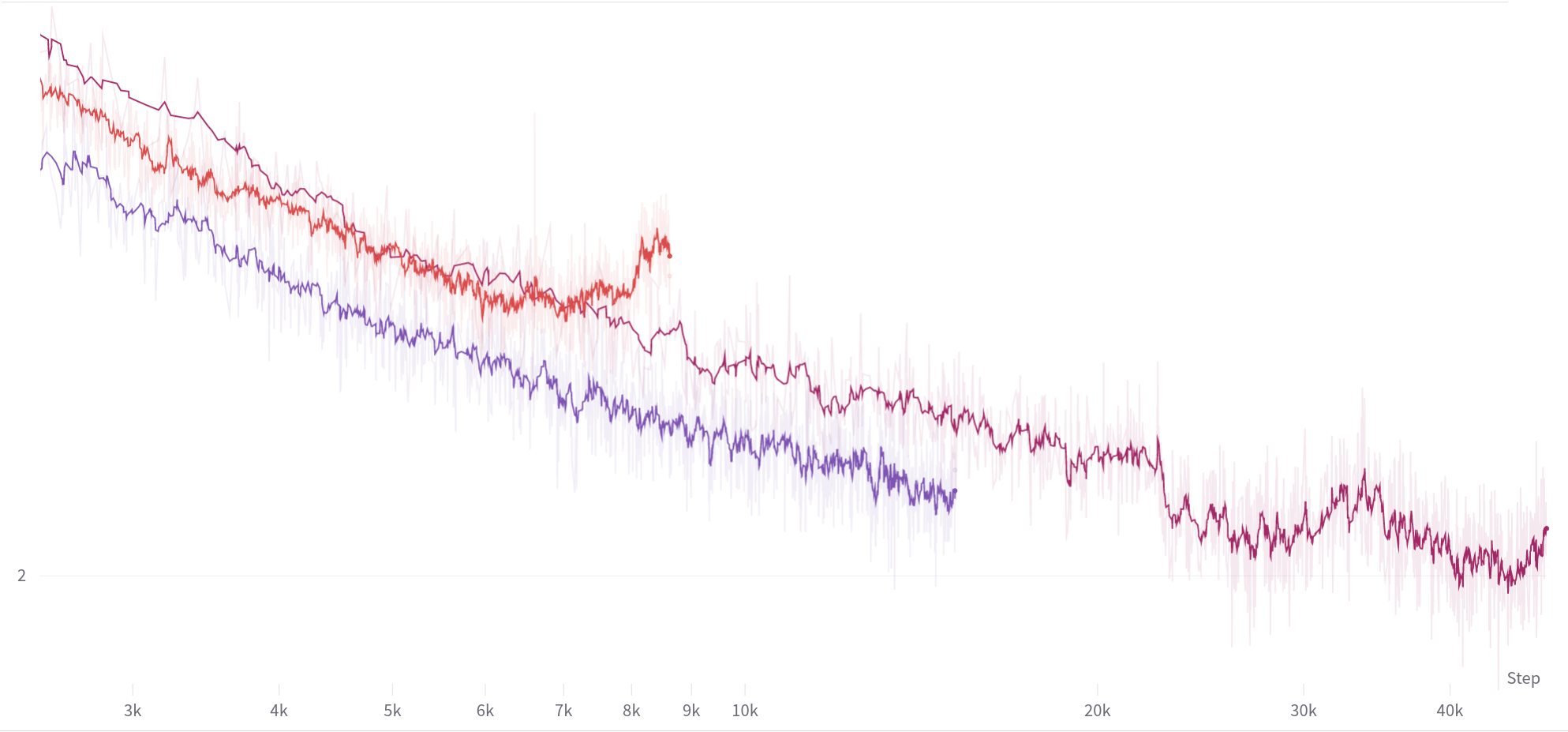
Two of them are normal runs. But let us pay attention to the red curve.
This is a 3B model diverged at a very early stage (~60k steps). Model specs:
| parameter count | context length | batch size | learning rate |
|---|---|---|---|
| 3B | 8192 | 8M tokens | 0.000256 |
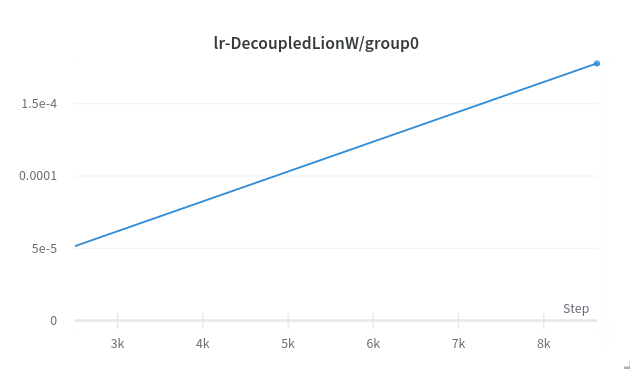
The optimizer is LionW and the weight decay is decoupled, meaning it is a fixed number instead of a quantity
proportion to the learning rate. In this case, I used 0.0000256, 10% of the max learning rate.
This was originally planned to be an ambitious run (trillion tokens) and it has a very slow warmup.
Weight decay adds an extra term in the loss function about the l2-norm of the parameters: $$ l´ = l + c|| \theta ||^2 $$ where $l$ is the original loss and $l´$ the $L2$-regularized loss.
Let us take a look at what happened to the $L2$-norm:
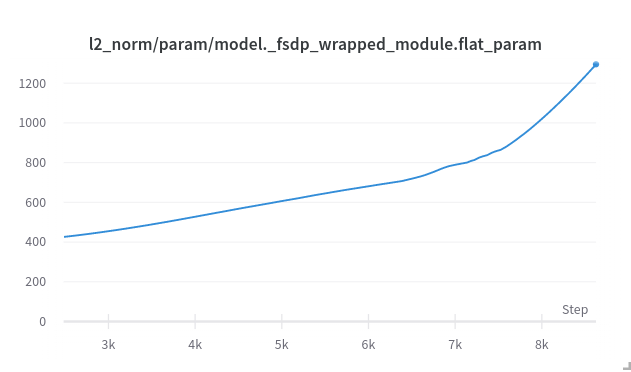
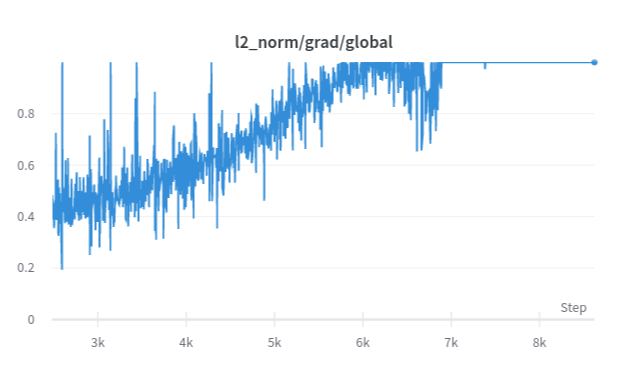
My overall theory is that, the bad calibration of learning rate leads the training to be trapped inside a sharp ditch in the loss landscape. The loss jumps higher by bumping against walls and the cliff gets sharper (higher and higher gradient norms). The chart of the l2-norm of the gradient also support this:
13B, mostly normal but…
The last one is not about a divergence, but a crazy pop of loss which miraculously recovered after 100 steps. It happens during learning rate annealing:
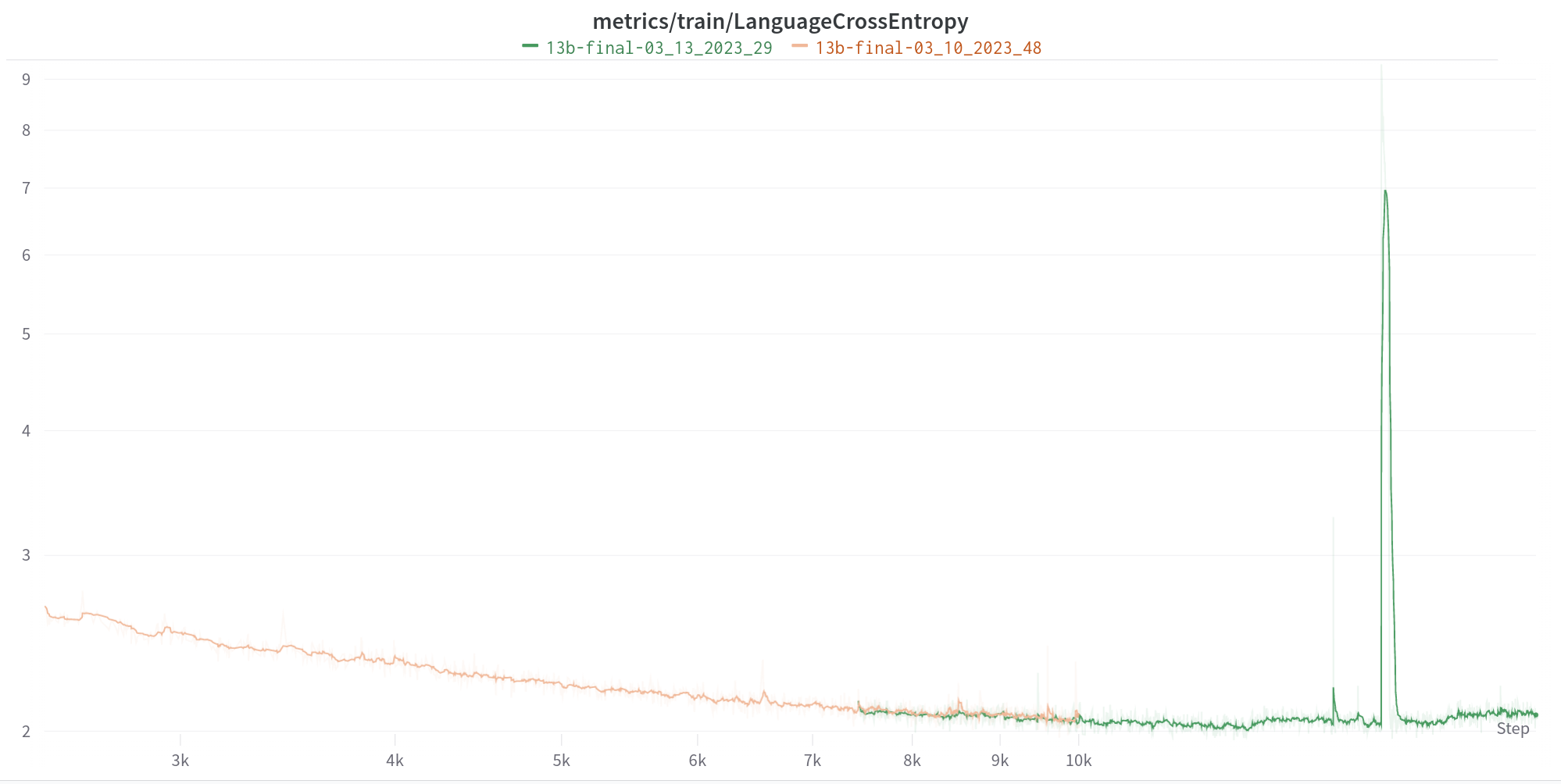
It is worth noting that similar loss spikes have been shown in a few papers of LLM trainings such as LLaMA (though far less severe than this).