MCTS and Theorem proving

With the increasing maturity of the Lean theorem prover, many people have attempted the combination of reinforcement learning (RL) and theorem proving. Among many attempts, the Hypertree proof search has been quite notable which I admire a lot personally.

Looking around, the general field of neural reasoning has also becoming a more prominent field since logical reasoning has been one of a few domains where LLM continues to struggle towards a satisfactory degree of reliability. A nice recent survey is this.

In this writing, I do not attempt to describe anything that outperforms something (which IMHO really kills the joy of research and an excess emphasis leads to a broad sense of “overfitting”). The goal is to jot down some thoughts and share some cool charts in my personal attempt of the “deep MCTS” + “Lean prover” approach. It needs to be noted that some related research collaboration is still up in the air. As a disclaimer, I do not share codes and I will only write about either 1. open-source materials or 2. strictly my own work.

Overview

As is commonly known, to implement something using RL, you just need to define a Markov Process which requires:

• An observation space;
• An action space;
• A reward function given an observation and an action.

The rough roadmap here is very clear:

• Define some sort of observations and actions around the Lean 4 engine, and use it as an iteration function.
• Use any signals but mostly focusing on the proof validity to define some sort of reward function.
• Plug in your favorite RL algorithm and profit.

There are many variants you can try in each step. It is quite doable to just come up with a weird combination to claim novelty. With some p-hacking, one can also publish a paper around it. But I am a dumb person and I stick to the dumbest plan:

• Narrow down the theorem proving task to a very small subset.
• Use a subset of tactics as the action space. And use a simple 0/1 reward on a successful sequence of tactics. Note that Hypertree proof search already did this, and people already tried to do RL on tactics in Lean 3 back in early 2020.
• Write a simple Lean 4 REPL wrapper that fits into the Gym (or nowadays it is called Gymnasium) library.
• Implement deep MCTS (i.e., some sort of AlphaZero)
  • Use the mctx which is a simple and highly modular library that handles vectorized tree search, backtracking, policy updating, etc.
  • Put in a neural network to do
    1. Inference - providing a prior;
    2. Training - distilling the MCTS-improved posterior.

Given that everybody and their mom starts to hear about LLM, I specifically chose transformer as the neural network. An observation will just be the theorem statement (e.g. “a ∧ b ↔ b ∧ a”), and it will be encoded by a custom tokenizer.

The logic side

Back in my math career, I have been having a (wrong) impression that:

1. we were still so far from formalizing the most recent and exciting math breakthrough such as the 20-century boom in Algebraic Topology and the monumental legacy of Grothendieck;
2. if auto-theorem-proving were to apply to anything at research-level, it will not be human-readable and help human researchers.

I trust that I was not alone. So you can imagine my shock when I first saw that the foundation of commutative algebra and algebraic geometry was nicely formalized in the community mathlib3. This is very similar to the AlphaZero-moment when a decade ago, you were probably told by your Olympiad Informatics coach that the game of Go cannot be solved in 50 years.

Back to the business. The most important scope to define is what theorems do the RL agents want to prove.

What to prove

Now, many people want to just reach AGI, so people just grab everything in the community mathlib because why not?

But do we really want to start with all domains in mathlib and train on all tactics? Do I first SFT on a random subset as seeds? Or do I restrict to a domain, or even a much smaller logical system to focus on more visible in-domain generalization?

Also, it leads to the question of sampling: how do we sample a theorem as the initial observation for the Lean engine? If we use synthesized theorems, how do we synthesize ground-truth theorem-proof pairs to either generate initial states or assist unsupervised RL by providing some baseline performance (due to the extreme sparsity of signals, some baseline-SFT is a very standard practice)?

I will not expand here to risk touching my colleagues’ works without consent. But here I just want to remark that

• Defining the scope of such project properly already requires a lot of understanding of mathematical logic, and is already a fun thing to keep your brain busy.

Here are some keywords of widely known concepts: first-order logic, propositional logic, deductive system, theorem generators. It is possible to come up with a comfortable restrictions and a nice theorem generator for some small-scale fun to work.

The action space

Now, let us say that we have a well-defined and closed subset of statements that Lean supports. Actions are tactics, but some tactics requires arguments. So we need to:

1. Write an IR (in my case, a Python IR) that

   • abstracts away symbols and expressions,
   • parses from Lean statements (states), and
   • renders into Lean statements.

   In other words, we build a simple IR mainly for parsing (because Lean does the dirty job of transformation for us).

2. Limit the number of variables (say, 10), and distinguish individual tactics that takes different variables (such as apply a, apply b, apply c, …).

We could try to find a very small logic system and countably many actions (due to unboundedness of variables) that are sufficient to prove every true statement. One of the challenges is that the length and the number of variables can grow during a proof, which make it unbound even during an episode. I am not aware of any result talking about an upper bound of necessary new variables given a set of tactics in a logic system.

But empirically, for some fun to happen, we can just settle with some arbitrary restrictions such as a maximum of 10 variables in a statement, and a maximum of 20 variables in the actions. Again, I do not intend to go into details in this part.

The reward

I am a big fan of simple 0/1 reward based on the final outcome. Sophisticated heuristics is not only unnecessary but also encouraging reward-hacking. Typical examples include a mild reward boost of shorter statement, or “hey, this action turns a true statement to an unprovable statement so let’s put a -100 reward for it!”. There are easily counter-arguments for each of artificial reward that does not come directly from the proof-checking engine.

In other words, heuristic-based rewards or fine-grained rewards usually work to a limited extent to battle either sparse signals or ambiguous goals. But it is usually not the ultimate solution for a fully unsupervised routine whose number of rollout need to scale.

The fun part - the experiments

Without being able to share codes and the exact setup, let us say that I am training a network who predicts a restricted set of tactics targetting a restricted but infinite set of basic logic statements where

• if the number of variables could have gone to infinite, the set of tactics would have been able to cover all proofs;
• there exists ways to algorithmically generate ground-truth proposition-proof pairs easily, though you cannot control what the proposition is until the end of the algorithm.

As mentioned, I implemented the JAX-version of deep-MCTS with the help of mctx library (but inevitably with a few monkey patches). To recall the standard procedure of deep-MCTS, it is to repeat the following cycle:

• Running inference on the network to provide
  1. a probability distribution of each action (tactic) as a prior.
  2. a value (here we choose the Q-value) of the current observation that aggregates future rewards in an exponentially-weighted manner.
• Running the MCTS for a fixed amount of times to improve the prior and form a posterior.
• Sample through the observations, collect many posteriors in a so-called “replay buffer” to form a set of training data consisting of many minibatches.
• Train and improve the network on the collected posterior.

In addition, a collection of more than 10k synthetic “theorems” are generated whose truthfulness is guaranteed. Also, their proofs are accessible, so one may choose to

• mix the ground-truth theorems into the initial replay buffer to provide early signals.

But since we have a healthy mix of difficulties (where many only needs 1-single application of a tactics), I did not adopt this method.

A couple key points regarding the synthetic theorems in my setup:

• The synthetic theorems serve as the initial states for the Lean engine. More precisely, every time the environment is reset, a random synthetic theorem is sampled as the initial observation.
• The model is never trained on an unprovable statement.

Evaluation

A hand-picked set of around 18 theorems are chosen with varying difficulties. It is also roughly ordered by difficulties so the first theorem requires the minimal amount of steps, and the last theorem takes more steps.

It is also made sure that they do not appear among the synthetic theorems.

Training metrics

Here is a combined picture of several training runs with different seeds and parameters.

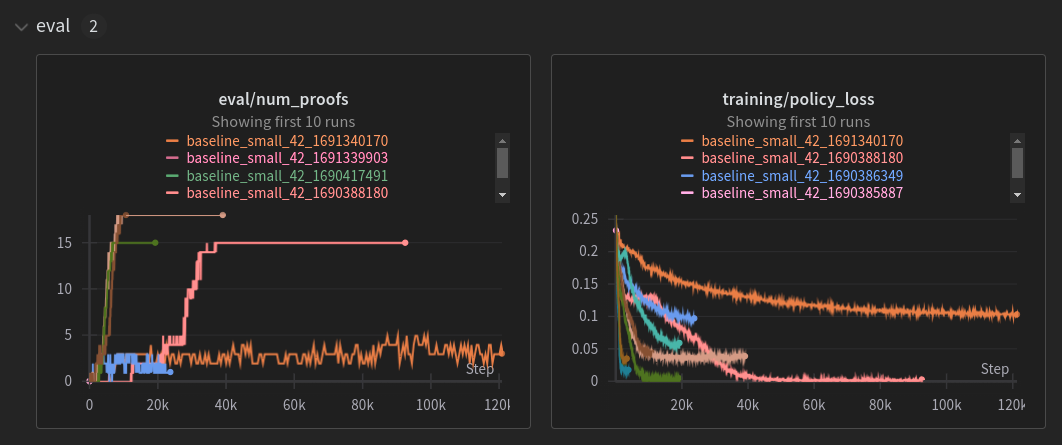
Here, “num_proofs” is the number out of the evaluation theorems that can be 0-shot proven by directly using the neural network policy. The overall policy loss function consists of the action-head cross-entropy loss and the MSE value loss.

We can see that the evaluation result roughly correlates with the policy loss. Also in the pink run, arguably the sharp increase in evaluation happens during the “double descent” where loss drop is temporarily accelerated.

A more fine-grained picture is the following.

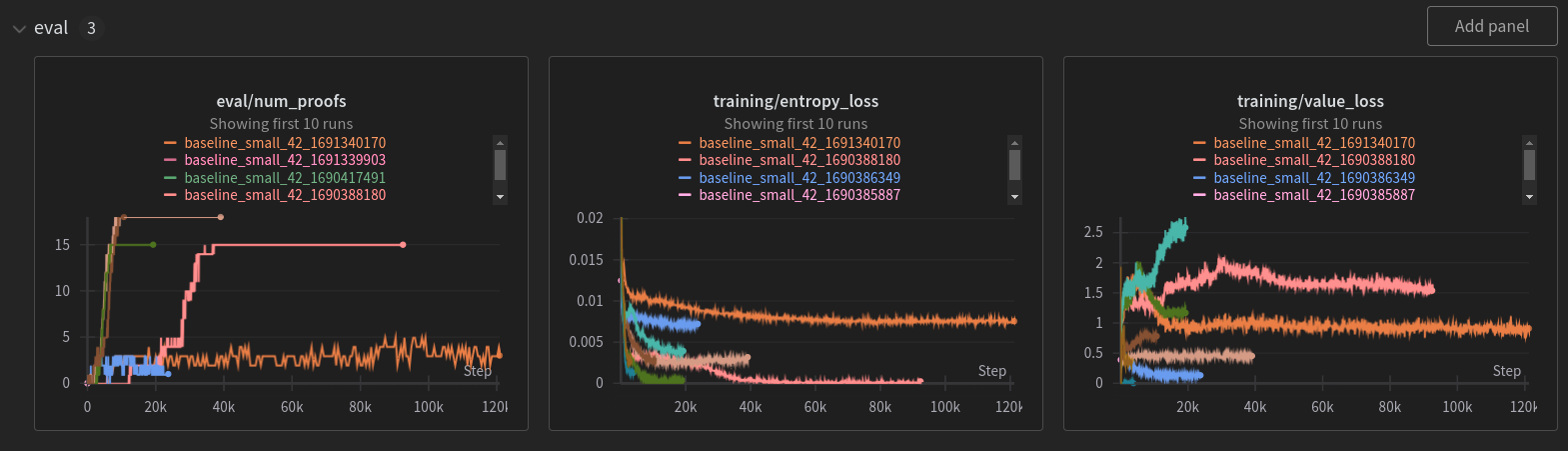
We can see that the value loss does not necessarily need to go down. A direct contribution is perhaps that the coefficient for the MSE value loss is too low. But turning it up seems to have negative impact. Value estimates are usually a moving target at early stage since it is largely policy-dependent and the policy keeps changing. So I can personally settle with not fully understanding its impact here.

Digging into one run, we can see how the evaluation evolves.

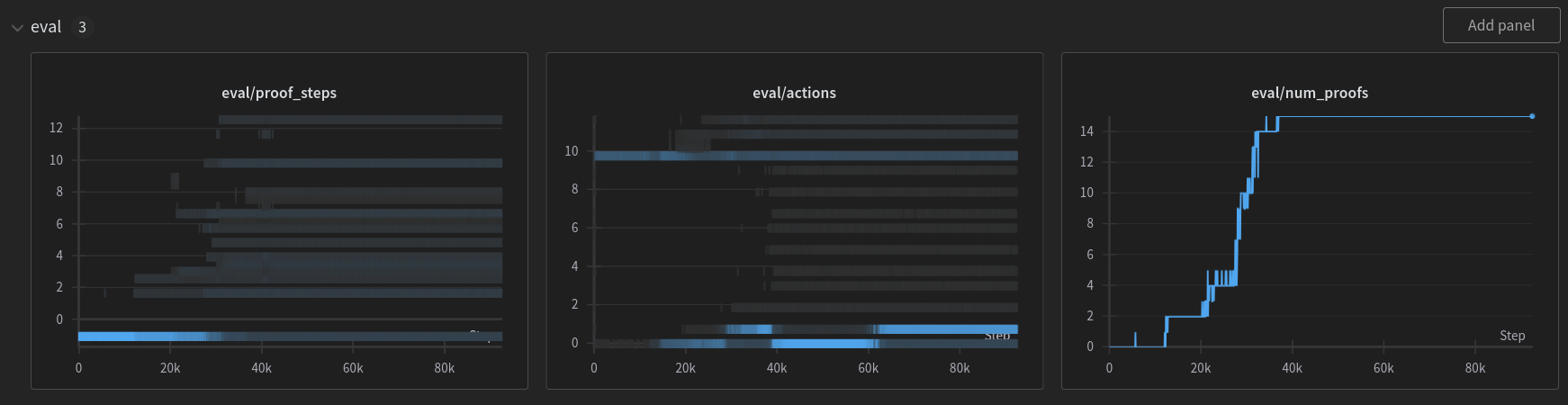
The “proof_steps” chart is how the proof length of each theorem (limited to 12) evolves over training. The more blue it shows, the longer its proof is.

We can see the first theorem starts out with the longest length, and gradually become shorting length. Also, easier theorem generally gets solved earlier (recall that they are roughly ordered by difficulties). And occasionally, the policy regresses (which the network will never know because the evaluation theorems are not among the synthetic initial observations).

Even more fun - playing with the trained agents

A big effort of mine is to code up the following command-line UI for investigating the policy of the trained network.

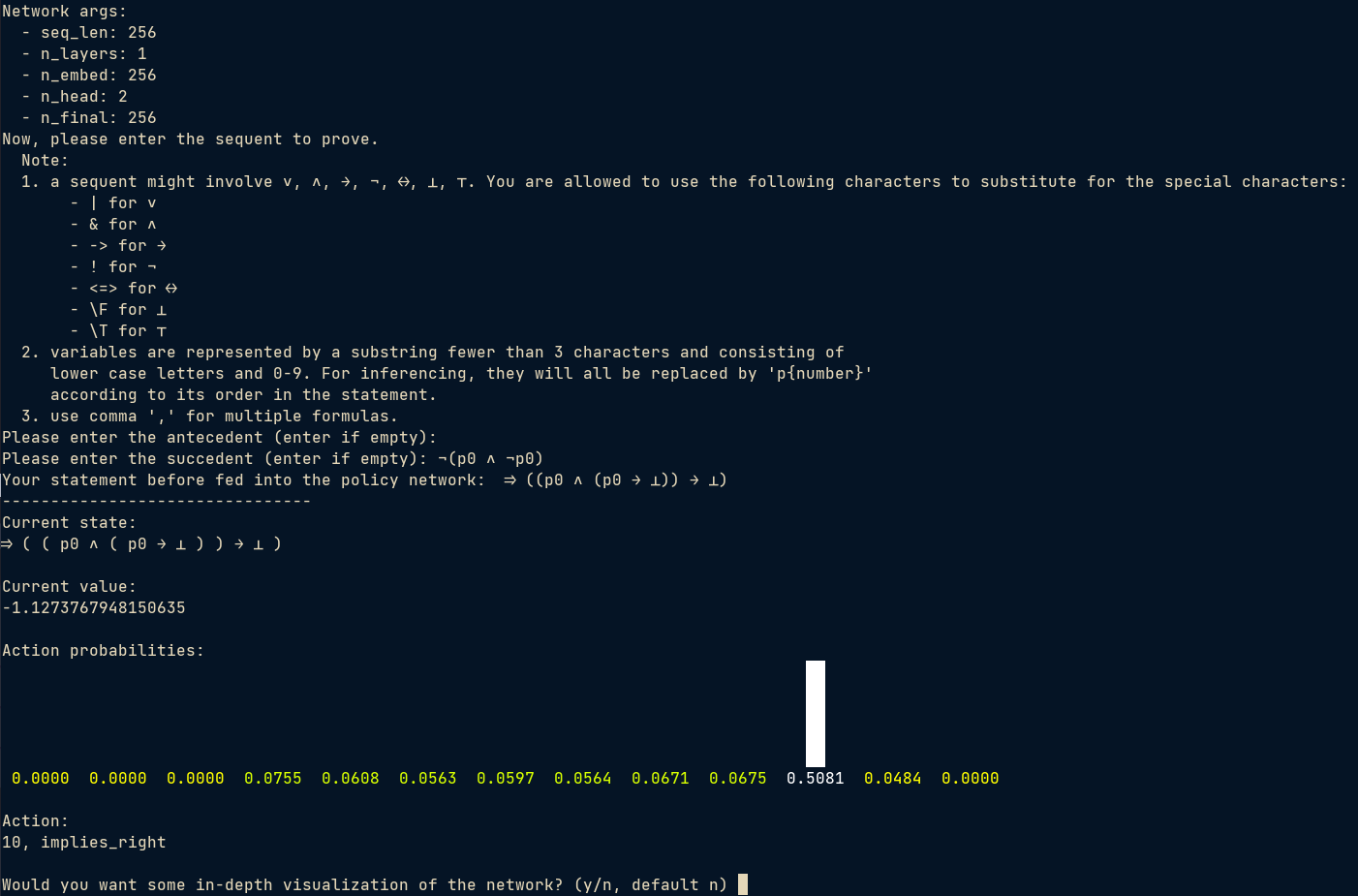
For this simple theorem, it still takes 2 steps to solve:

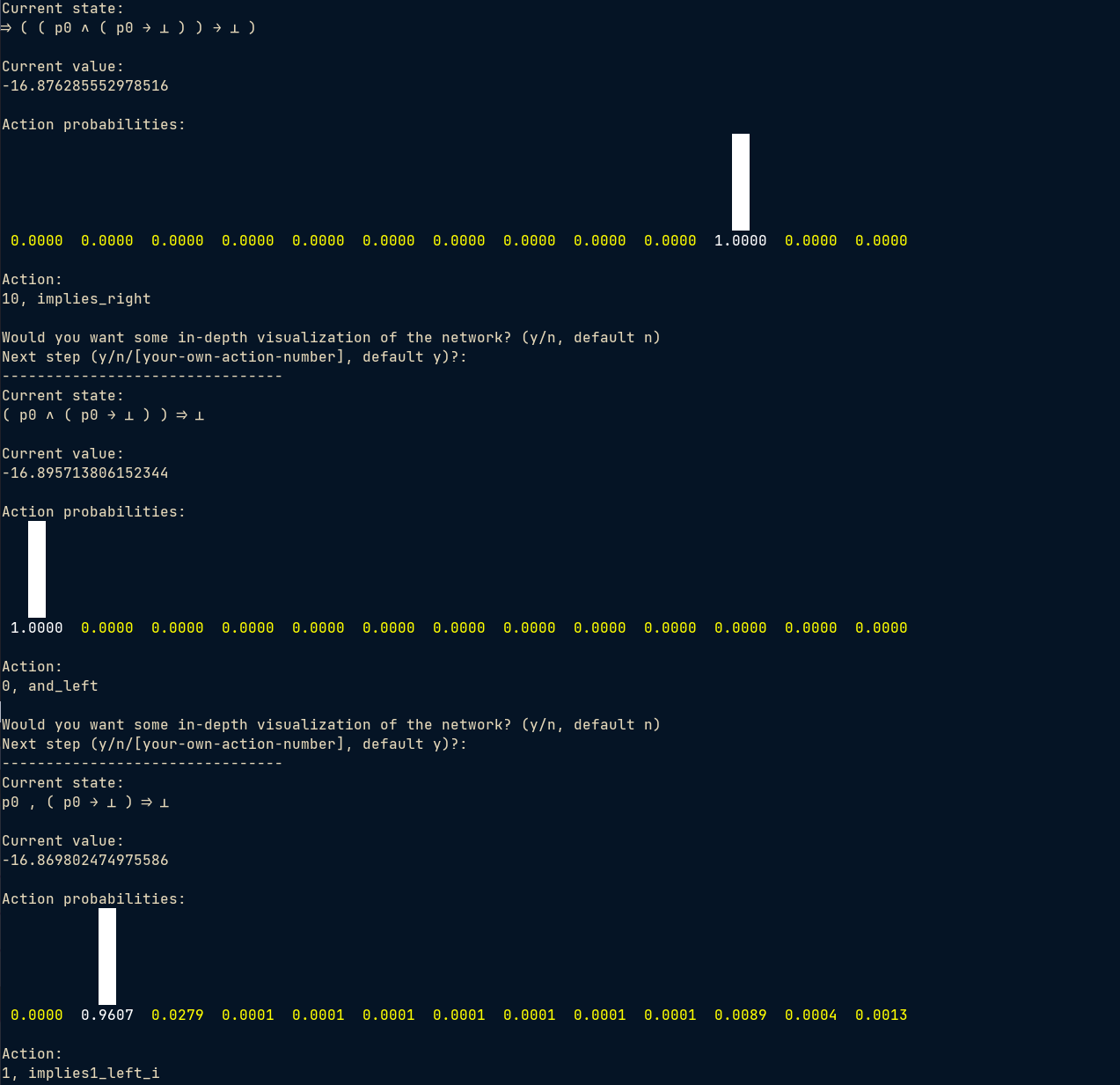
One may notice that the network is fairly certain about its choice in such simple cases. In fact, for most of the simple theorems that I can type and manually verify, it can reach some sort of proof with such a degree of confidence.

Generalize from true statements to unprovable statements

An artifact of being only trained on true statements is that it captures structural similarities and generalize to unprovable statements. Not saying it is bad (because it is simply ill-defined to ask Lean engine tactics to operate on an unprovable statement), but may be cool to watch a simple example:

(a->b) => (a->b) is a trivial statement and it solves it using two steps.

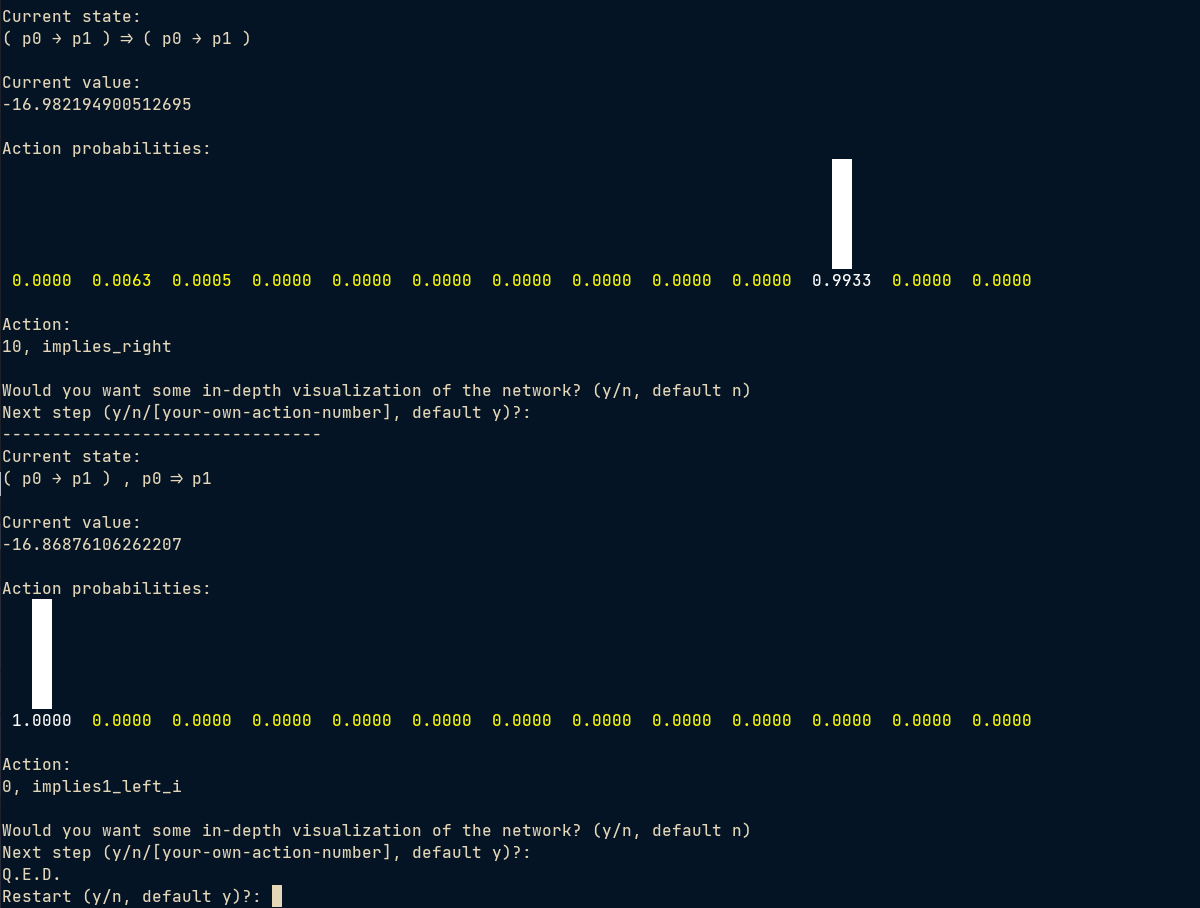
But I can easily change it into (a->b) => (b->a) which is unprovable. Turns out the model gave a very similar solution.

As a matter of fact, the attention weights already show that the model confuse the two cases big time (first-layer first-head):

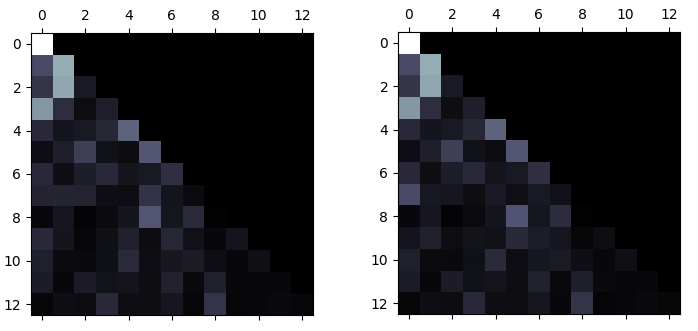
This is the picture of attention weights side-by-side for (a->b)=>(a->b) and (a->b)=>(b->a). Can you spot the differences?

On the other hand, this may also indicate that the model relies heavily on pattern matching, maybe using general structure signals such as brackets and operators.

Uncertainty on unprovable statements

When it is evaluated on some out-of-distribution(OOD) data samples (unprovable statement), it can “show hesitance”. It is generally well-known that the classification predictions tend to have a higher entropy on OOD samples.

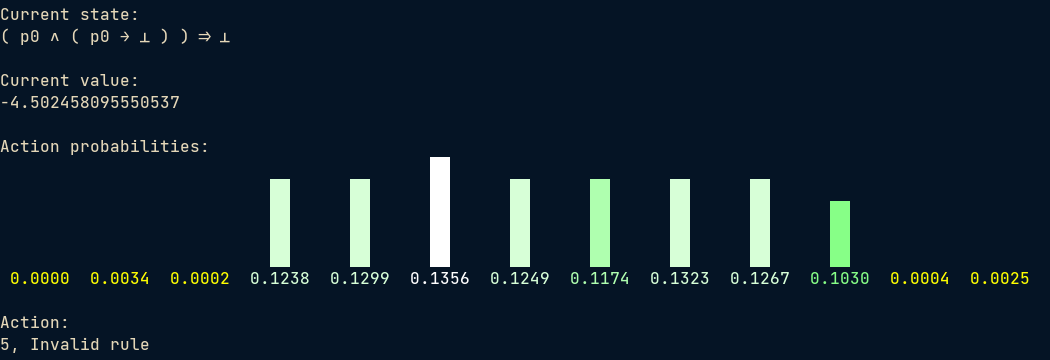
Attention

Here is the first-layer and first-head attention weight under the following sequence:

position: 0    1    2    3     4    5    6     7    8    9   10   11   11   12   13     14
token:   '⇒', '(', '(', 'p0', '∧', '(', 'p0', '→', '⊥', ')', ')', '→', '⊥', ')', '\n', '[END]'

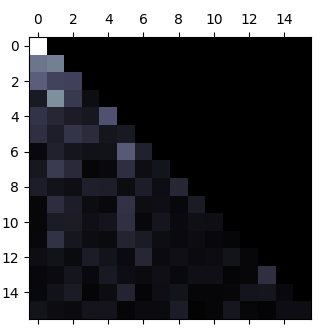
Not sure how much can be read into it, one notable thing is that the first layer attention tends to use open or close bracket as a pivot (here the lighter vertical is at position 5 corresponding to the ‘(’ after the ‘∧’.

Final words

Overall, this is not a fully-fledged research paper and I am merely sharing the fun. Plus that this is a single highly-overfit model with a not-so-careful experiment setup. But I personally think that many thought-provoking questions are surfacing and screaming further study.